Optimally Grouping cards in Rummy — Tips, Tricks and an Algorithmic approach with Code

All About Indian Rummy

Rummy is a card game played with two decks of cards, including the two Jokers. To win the game, a player must make a valid declaration by drawing and discarding cards from two piles: a closed deck, where the player cannot see the card they are picking, and an open deck, which consists of cards discarded by players. To win, players need to arrange their cards into valid sequences and sets.

We will discuss in detail on how to maximize wins and minimize losses in the game of Rummy.

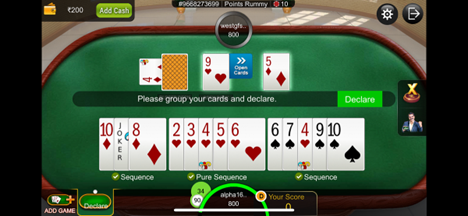
Terminologies

• Card: A playing card with a rank (1–13) where 11–13 are face cards (J, K, Q) and a suit(♣,◆, ♥, ♠).
• Printed Joker Card: Two special cards apart from 52 cards of the deck that can substitute for any card in a player’s hand.
• Wild Card: A special card drawn at the start of the game that acts similar to the printed joker and can substitute for any card in a player’s hand.
• Pure Sequence (PS): A set of 3 and more cards with consecutive ranks and the same suit. For example, (4♥, 5♥, 6♥, 7♥, 8♥) is a Pure Sequence of length 5, featuring consecutive ranks (4, 5, 6, 7, 8) and the suit ♥.
• Impure Sequence/Sequence (IS or Seq): A set of3 or more cards with consecutive ranks and the same suit, including one or more Joker cards. For instance, (J♥, 5♣, K♥, A♥) is an Impure Sequence of length 4,with 5♣ serving as the Joker card.
• Set: A combination of 3 or 4 cards with the same rank but different suits. For example, (J♣, J◆, J♥, J♠) is a Set of 4cards, all with the rank 11 but with four different suits.
• Invalid: Any card combination that does not fit into any of the categories above (PS, IS, Set) is considered Invalid.
• Meld: Any combination of cards that is either a PS, IS, Set, or Invalid.
• ‍Valid Declaration: A grouping with no Invalid melds and at least 2 Sequences, with at least one being a PS. The remaining melds can be any type (PS, IS, Set).‍
• Open Deck: A stack of face-up cards placed on the table from which players can draw during their turns. This pile is visible to all players, enabling them to make strategic decisions based on the cards shown. It is also referred to as the Discard Pile.‍
• Closed Deck: A stack of face-down cards remaining after dealing. The cards are arranged randomly and their identities are hidden from the players. Players draw from this deck without knowing which cards they will receive.

How to Play Rummy

Creating valid sequences and sets can be challenging, as the number of combinations increases exponentially with each card dealt to the player, having an upper bound of 13! combinations.

The Point System in Rummy can be found at Rummy Circle.

Tips and Tricks

1. Once the cards are dealt, start grouping them to create both pure and impure sequences; otherwise, it will be more challenging to minimize your points as the game progresses.
2. Focus on hands that include at least one joker along with a pure sequence, as this combination often gives you an advantage early in the game, making it easier to reduce your points.
3. Keep a close eye on what your opponents are selecting from the open deck, as it can offer insights into their hands and what they’re aiming to form.
4. At the start of the game, evaluate the potential for forming pure and impure sequences with your cards. The more cards you have that can help create these sequences, the better your chances of minimizing points.
5. Based on your initial grouping, decide whether to drop the hand. Use the strategies discussed to guide your choice on whether to continue playing.

Therefore, it’s crucial to optimally group your cards with each move to minimize points, which increases your chances of winning and reduces potential losses if you do end up losing.

More tips and tricks here —  https://www.rummycircle.com/how-to-play-rummy/rummy-tips-tricks.html

Algorithmic approach to Optimal Grouping

Since our goal is to combine cards in away that minimizes points, this becomes a combinatorial problem. It can be effectively solved using Dynamic Programming with Bitmask.

Brute Force Approach

The brute force solution involves checking all permutations and grouping the cards into lengths of 3 to 5 for pure and impure sequences, and lengths of 3 to 4 for sets. To illustrate, let’s simplify this with an example using 7 cards instead of 13.

Given hand: 6♣, 7♣, 8♣, 7♠, 9♠, 10♠, 8♠.

There are 7! permutations possible. For example:

• (6♣, 7♣, 8♣, 7♠, 9♠, 10♠, 8♠)
• (6♣, 7♣, 7♠, 8♣, 9♠, 8♠, 10♠)
• (6♣, 7♣, 8♣, 7♠, 8♠, 9♠, 10♠), and so on.

Possible groupings length could be (3, 3, 1), (3, 4) and (5,2). We explain these lengths below.

Let’s take the last permutation (6♣, 7♣, 8♣, 7♠, 8♠, 9♠, 10♠) and consider the grouping (3, 3, 1):

• ‍Meld 1:First 3 cards (6♣, 7♣, 8♣) → Points = 0 (pure sequence).
• ‍Meld 2:Next 3 cards (7♠, 8♠, 9♠) → Points = 0 (pure sequence).
• ‍Meld 3:Last card (10♠) → Points = 10 (invalid).

Total points = 0 (Group 1) + 0 (Group 2)+ 10 (Group 3) = 10 points.

Now, using the same permutation (6♣, 7♣,8♣, 7♠, 8♠, 9♠, 10♠) with the grouping (3, 4):

• ‍Meld 1:First 3 cards (6♣, 7♣, 8♣) → Points = 0 (pure sequence).‍
• Meld 2:Next 4 cards (7♠, 8♠, 9♠, 10♠) → Points = 0 (pure sequence).

Total points = 0 (Group 1) + 0 (Group 2) = 0, making this an optimal grouping.

Permutations to check 13! * 8 = 49816166400, taking approximately 1.5 hours. Don’t worry we discuss a solution that runs under 10 milliseconds.

Dynamic Programming with Bitmask

The brute force approach is impractical for real-time assistance to players due to its complexity. To improve upon this, we can leverage dynamic programming with bit-masking, which helps manage overlapping subproblems and enables efficient memorization.

Let’s go through the logic along with python code. We provide the helper functions below.

Imports:

import numpy as np
import copy
import random
import itertools
from scipy.ndimage import shift

Hand points calculation logic:

‍

# locations - store the locations of the card in the hand
# hand_array - store the hand as a tuple of suit and card
# hand - store the hand as array of string# joker - joker card
def calculcate_hs(locations,hand_array,hand,joker):
   sc = 0
   for loc in locations:
       if not (hand_array[loc][0] == -1 or hand_array[loc][1] == int(joker[:-1])):
           if hand_array[loc][1] == 1:
               sc+=10
           else:
               sc+=min(10,hand_array[loc][1])
   return sc

Get count of cards already processed:

# get the number of the cards that has been considered in the hand
def get_len(num):
   s=0
   while num!=0:
       s+=(num & 1)
       num = num>>1
   return s

Get the location of the cards already considered:

# get all the cards position that are considered in the hand
def get_set_pos(num):
   i = 0
   pos = []
   while num!=0:
       if (num & 1) == 1:
           pos.append(i)
       num = num>>1
       i+=1
   return pos

Make a suit to cards and cards to suit mapping present in the hand:

# get suit to card mapping dictionary both including and excluding the wild card

# get suit to card mapping dictionary both including and excluding the wild card
def get_suit_card_mapping(hand0,joker):
   different_suits = {'h':[], 's':[], 'c':[], 'd':[]}
   different_suits_without_joker = {'h':[], 's':[], 'c':[], 'd':[]}
   for i,card in enumerate(hand0):
       initial = card[0]
       remaining = int(card[1:])
       different_suits[initial].append(remaining)
       if card in joker or card == 'j':
           continue
       else:
           different_suits_without_joker[initial].append(remaining)
   for card_type in different_suits:
       different_suits[card_type] = sorted(different_suits[card_type])
       different_suits_without_joker[card_type] = sorted(different_suits_without_joker[card_type])
   return different_suits,different_suits_without_joker
# get card to suit mapping dictionary
def get_card_suit_mapping(hand0,joker):
   different_suits = {1:[], 2:[], 3:[], 4:[], 5:[], 6:[], 7:[], 8:[], 9:[], 10:[], 11:[], 12:[], 13:[]}
   for i,card in enumerate(hand0):
       initial = card[0]
       remaining = int(card[1:])
       if card in joker or card == 'j':
           continue
       else:
           different_suits[remaining].append(initial)
   return different_suits

Store all the hash in relevant meld type — Pure Sequence, Impure Sequence and Sets.‘typ’ 1 is pure sequence, ‘typ’ 2 is impure sequence and ‘typ’ 3 are sets in the code below:

# add cards which are considered in the hand based on type pure seq/impure seq/set in the good hands which will be part of the optimal grouping

# add cards which are considered in the hand based on type pure seq/impure seq/set in the good hands which will be part of the optimal grouping
def mark_location(comb,loc_mapping,idx,mask,good_hands,typ):
   if len(comb) == idx:
       good_hands[typ].add(mask)
   else:
       if type(comb[idx]) == tuple:
           pos = 2**comb[idx][1]
           mark_location(comb,loc_mapping,idx+1,mask+pos,good_hands,typ)
       else:
           for i in loc_mapping[comb[idx]]:
               pos = 2**i
               mark_location(comb,loc_mapping,idx+1,mask+pos,good_hands,typ)

Lets Begin,

First, let’s explore the combinatorial aspect of this problem. Since each player is dealt 13 cards, we can represent each card with a unique bit which behaves as a hash for the card, resulting in ²¹³ = 8192 possible combinations for card selection. For example, if a player has the hand (5♣, 6♣, 7♣, 8♣, 9♣, 7♠, 8♠,9♠, 10♠, J♥, K♥, A♥, K♦), we can assign bits as follows:

• 5♣ is represented by the 0th bit and can be represented as ²⁰ = 1,
• 6♣ by the 1st bit and can be represented as ²¹ = 2,
• 7♣ by the 2nd bit and can be represented as ²² = 4,
• 8♣ by the 3rd bit and can be represented as ²³ = 8,
• 9♣ by the 4th bit and can be represented as ²⁴ = 16

and so on for the remaining cards.

We have established a method to uniquely represent and identify each card in the hand. Now, let’s discuss how to represent melds. For instance, consider the first three cards of the hand mentioned earlier — (5♣, 6♣, 7♣). We can create a unique hash for this meld by adding the unique representations of each card: (1+ 2 + 4) = 7. This sum represents the unique hash for the meld (5♣, 6♣, 7♣).

Now, let’s see how we store the melds using these hashes. Consider the hand (5♣, 6♣,7♣, 8♣, 9♣, 7♠, 8♠, 9♠, 10♠, J♥, K♥, A♥, K♦):

1. Hash for the pure sequence (5♣, 6♣, 7♣, 8♣, 9♣):
       (1 + 2 + 4 + 8 + 16) = 31
2. Hash for the pure sequence (7♠, 8♠, 9♠, 10♠):
       (32 + 64 + 128 + 256) = 480
3. Hash for the pure sequence (J♥, K♥, A♥):
       (512 + 1024 + 2048) = 3584
4. Hash for the last invalid meld (K♦):
       (4096) = 4096

To find the total hash for the hand, we sum these values:
31 + 480 + 3584 + 4096= 8191.
As you can see that grouping cards and calculating the hash will always sum to 8191. We can conclude that if we permute through all the combinations of meld in the hand and sum up their hash, we will get 8191 giving us a way to memorize all possible pure sequences, impure sequences and sets.

Steps of the algorithm

To determine the optimal grouping and points for the hand, we can follow these steps:

Find All Possible Pure Sequences:

• Generate pure sequences of lengths3 to 5 and store their hashes.
• If no pure sequences are found, calculate the total points for the hand.

Check for Impure Sequences:

• If at least one pure sequence exists, find all possible impure sequences and store their hashes.
• If no impure sequences are found, check for non-overlapping pure sequences calculated in Step 1. If none are found, calculate the points for the cards not included in the only pure sequence.

Evaluate Non-Overlapping Pure Sequences:

• If there are at least two non-overlapping pure sequences or one pure and one impure sequence, identify all possible sets in the hand and store their hashes.

Dynamic Programming Approach:

• Once all sets and sequences are calculated, utilize dynamic programming to explore all valid combinations of these sets and sequences, optimizing for the lowest total points.

By systematically approaching the problem in this manner, we ensure that we coverall potential combinations and can determine the best grouping of cards effectively.

Lets Code the algorithm,

Let’s illustrate the pre-processing of a hand by converting it into mappings of suit to card and card to suit.

# hand of the user
hand = ['1h', '2h', '3h', '4h', '1h', '2h', '3h', '4h', '4d', '12h', '13h', '5h', 'j']
# wild card
joker = '4d'
if joker == 'j':
   joker = '1h'
# pre-processing of the hand and joker
hand_inverted = [card[-1]+card[:-1] if len(card)>1 else 'j' for card in hand]
hand_array = [[card[-1],int(card[:-1])] if len(card)>1 else [-1,20] for card in hand]
joker_inverted = ['s'+joker[:-1],'c'+joker[:-1],'d'+joker[:-1],'h'+joker[:-1]]
hand_temp = []
all_jokers = []
loc_mapping = {}
for i,h in enumerate(hand_inverted):
   if h in joker_inverted or h == 'j':
       all_jokers.append((h,i))
   if h in loc_mapping:
       loc_mapping[h].append(i)
   else:
       if h != 'j':
           hand_temp.append(h)
       loc_mapping[h] = [i]
hand_inverted = hand_temp
different_suits,different_suits_without_joker = get_suit_card_mapping(hand_inverted,joker_inverted)
different_cards = get_card_suit_mapping(hand_inverted,joker_inverted)
good_hands = {1:set(),2:set(),3:set()}
# calculate initial hand score
output = [calculcate_hs(range(len(hand)),hand_array,hand,joker),[2**i for i in range(0,len(hand))]]
final_output = []

Find All Possible Pure Sequences, we get pure sequences and convert it to a hash and store it into a map.

# logic to get all possible pure sequences in the hand
def get_pure_sequences(different_suits):
   all_possible_pure_seqeunces = []
   for length in range(3,6):
       for card_type,cards in different_suits.items():
           current_seq = []
           if 1 in cards:
               cards = cards + [14]
           for card in cards:
               if len(current_seq) == 0 or current_seq[-1]+1 == card:
                   current_seq.append(card)
               else:
                   current_seq = [card]
               if len(current_seq)==length:
                   all_possible_pure_seqeunces.append([f"{card_type}{1 if i == 14 else i}" for i in current_seq])
                   current_seq = current_seq[1:]
   return all_possible_pure_seqeunces
# we first look for at least one pure sequences
seq = get_pure_sequences(different_suits)
# we store all the pure sequences in a map
for i in seq:
   mark_location(i,loc_mapping,0,0,good_hands,1)

Implementing Check for Impure Sequences and Evaluate Non-Overlapping Pure Sequences, we get impure sequences and if impure sequences exist we also calculate sets. We convert it to a hash and store it into a map as we did for the pure sequences above.

Helper function to check whether a sequence is impure or not and to get all possible sets.

# function to check where a sequence is an impure sequence or not.
def check_impure_seq(l,jokers):
       if len(l)>1:
           d = shift(l,1,cval=l[0]-1)+1
       else:
           d = l
       s = sum(l-d)
       if s<=len(jokers):
           return s
       elif 1 in l:
           l[l==1] = 14
           l = np.sort(l)
           if len(l)>1:
               d = shift(l,1,cval=l[0]-1)+1
           else:
               d = l
           s = sum(l-d)
           if s<=len(jokers):
               return s
       return -1
# function to get all possible sets in the hand
def get_sets(different_suits,all_jokers,joker_combinations):
       all_possible_sets = []
       # below we generate combinations for cards with same number but different suits
       for card in different_suits:
           if len(different_suits[card]) >= 3:
               for length in range(3,len(different_suits[card])+1):
                   combs = itertools.combinations(different_suits[card],length)
                   for comb in combs:
                       s = []
                       for val in comb:
                           s.append(str(val)+str(card))
                       all_possible_sets.append(s)
       # below we generate combinations for cards with same number but different suits and also including the joker
       for length in range(max(2,3-len(all_jokers)),4):
           for joker_length in range(max(1,3-length),min(4-length+1,len(all_jokers)+1)):
               for card,card_type in different_suits.items():
                   if len(card_type)>=length:
                       combs = list(itertools.combinations(card_type,length))
                       for comb in combs:
                           current_seq = []
                           for val in comb:
                               current_seq.append(str(val)+str(card))
                           for item in joker_combinations[joker_length-1]:
                               all_possible_sets.append(current_seq+list(item))
       return all_possible_sets

We iterate through all the combinations involving the joker and check if it is an impure sequence or not.

# Now we create optimal hands based on valid declarations.
# if we have at least one pure sequence then only we can make a valid declaration.
if len(seq)>0:
   set_flag = False
   # Now we check if there is at least one impure sequence or non-overlapping pure sequence.
   joker_combinations = [list(itertools.combinations(all_jokers,i)) for i in range(1,min(6,len(all_jokers)+1))]
   if len(all_jokers)>0:
       seq = []
       for t in range(2,len(joker_combinations)):
           for p in joker_combinations[t]:
               seq.append(list(p))
       for card_suit,cards in different_suits_without_joker.items():
           for x in range(max(1,3-len(all_jokers)),5):
               vals = itertools.combinations(cards,x)
               for val in vals:
                   val = list(val)
                   t = check_impure_seq(np.array(val),all_jokers)
                   tt = [f"{card_suit}{itr}" for itr in val]
                   if t != -1:
                       for i in range(max(1,t)+max(0,(3-x)-1),min(5-x+1,len(all_jokers)+1)):
                           for p in joker_combinations[i-1]:
                               seq.append(tt+list(p))
       for i in seq:
           mark_location(i,loc_mapping,0,0,good_hands,2)
       good_hands[2] = good_hands[2]-good_hands[1]
       # if there is an impure sequence we look for sets in the hand.
       if len(seq)>0:
           set_flag = True
           seq = get_sets(different_cards,all_jokers,joker_combinations)
           for i in seq:
               mark_location(i,loc_mapping,0,0,good_hands,3)
   # if we have at least two pure sequences and sets in the hand.
   if len(seq)>1 and not set_flag:
       seq = get_sets(different_cards,all_jokers,joker_combinations)
       for i in seq:
           mark_location(i,loc_mapping,0,0,good_hands,3)
# code below is part of the if block of the pure sequence which is
# the first if block of this section.

Continuing in the same if section as above, we perform memorization of each meld and store the best possible valid combination with each grouped meld.

# in the same if block as above.
   ans = [200]*2**len(hand)
   optimal_hand = [None]*2**len(hand)
   # Below we look for a set of non-overlapping pure/impure/sets that gives the minimum score.
   def get_permutation(current_hand,optimal_hand,ans,hand_array,hand,joker,good_hands):
       if current_hand == 0:
           return 0, []
       elif ans[current_hand] != 200:
           return ans[current_hand],optimal_hand[current_hand]
       else:
           flag = False
           for tc in [1,2,3]:
               for pos in good_hands[tc]:
                   if pos&current_hand == pos:
                       flag = True
                       nscore,o = get_permutation(current_hand^pos,optimal_hand,ans,hand_array,hand,joker,good_hands)                       
                       if nscore<ans[current_hand]:
                           ans[current_hand] = nscore
                           optimal_hand[current_hand] = [pos] + o
           if not flag:
               pos = get_set_pos(current_hand)
               nscore = calculcate_hs(pos,hand_array,hand,joker)
               ans[current_hand] = nscore
               optimal_hand[current_hand] = [current_hand]
           return ans[current_hand],optimal_hand[current_hand]
   # below we map the hash to the card and calculate the hand score.
   hand_max = 2**len(hand)-1
   for j in good_hands[3]:
       ans[j] = 0
       optimal_hand[j] = [j]
   for i in good_hands[1]:
       ans[i] = 0
       optimal_hand[i] = [i]
       left_hand = hand_max^i
       score = calculcate_hs(get_set_pos(left_hand),hand_array,hand,joker)
       if score<output[0]:
           output[0] = score
           output[1] = [i] + [left_hand]
   for j in good_hands[2]:
       ans[j] = 0
       optimal_hand[j] = [j]
   flag = False
   for i in good_hands[1]:
       for j in good_hands[2]:
           if i&j==0:
               ans[i|j] = 0
               optimal_hand[i|j] = [i,j]
               score,oh = get_permutation(hand_max^(i|j),optimal_hand,ans,hand_array,hand,joker,good_hands)
               if score<output[0]:
                   output[0] = score
                   output[1] = [i,j] + oh
               if score == 0:
                   flag = True
       if flag:
           break
       for j in good_hands[1]:
           if i&j==0:
               ans[i|j] = 0
               optimal_hand[i|j] = [i,j]
               score,oh = get_permutation(hand_max^(i|j),optimal_hand,ans,hand_array,hand,joker,good_hands)
               if score<output[0]:
                   output[0] = score
                   output[1] = [i,j] + oh
               if score == 0:
                   flag = True
       if flag:
           break
   for output_hand in output[1]:
       h = []
       for location in get_set_pos(output_hand):
           h.append(hand[location])
       final_output.append(h)
print('Grouped Hand = ' + str(final_output))
print('Hand Points = ' + str(min(80,output[0])))

The above code has a computational complexity of 2¹³ + 2¹³ + 2¹³= 24576 with average case complexity of Θ(2¹³) and runs under 10 milliseconds.

Conclusion

We’ll explore the most popular online RMG of Rummy, sharing tips and tricks to maximize wins and minimize losses. We’ll also address the challenge of optimal grouping using dynamic programming with bit-masking, along with the relevant code.

‍